Wikipediya, ensiklopediya xosere ra
parabolê y=x2 yew het hereketê dereca 360 ra eksenê paraboli de geyreno Parabol ( Yunanki :παραβολή - tatbik ) namey fonksiyono kvadratiko ke serê grafikê (y = x²) dero. Parabol cebır de namey fonksiyono ke dereca II. rao, namey eyo. Formulê paraboli f(x) = ax2 + bx + c o. Eno parabol de apsisê noxtay ke eksenê y cıra keno 0o u ordinatê cı f(0) = c o. Eno denklem de formulê diskriminanti D = b2 – 4ac o u eke ;
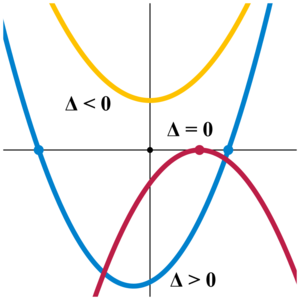
eke D > 0 ; parabol eksenê x noxtay dı de cıra keno.
eke D < 0 ; parabol eksenê x cıra nêkeno.
eke D = 0 ; parabol eksenê x ra tena temas keno. Sistemê koordinatio kartezyeni de denklemê paraboli y=ax^2+bx+c o. Herfa a hetê parabolio. Eke herfa a>0 ermeyê paraboli cor dero, eke herfa a>0 ermeyê paraboli cêr dero.
Formülê noxtay parabolio pil enayo ;
r
=
−
b
2
a
{\displaystyle r={\frac {-b}{2a}}}
k
=
f
(
r
)
=
4
a
c
−
b
2
4
a
{\displaystyle k=f(r)={\frac {4ac-b^{2}}{4a}}}
y
=
f
(
x
)
=
a
(
x
−
r
)
2
+
k
{\displaystyle y=f(x)=a(x-r)^{2}+k}
r
(
φ
)
=
4
a
cos
(
φ
)
sin
2
(
φ
)
φ
∈
[
−
π
2
,
π
2
]
∖
{
0
}
.
{\displaystyle r(\varphi )=4a{\frac {\cos(\varphi )}{\sin ^{2}(\varphi )}}\quad \ \varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}.}
(
a
,
0
)
{\displaystyle (a,0)}
r
(
φ
)
=
2
a
1
−
cos
(
φ
)
φ
≠
2
π
k
.
{\displaystyle r(\varphi )={\frac {2a}{1-\cos(\varphi )}}\quad \ \varphi \neq 2\pi k.}
Gorey cayê deltay ra işaretê deltay
x
2
+
2
x
h
+
h
2
=
(
x
+
h
)
2
.
{\displaystyle x^{2}+2xh+h^{2}=(x+h)^{2}.\,\!}
denklemê mısali ;
a
x
2
+
b
x
+
c
=
0
{\displaystyle ax^{2}+bx+c=0\,\!}
x2
x
2
+
b
a
x
+
c
a
=
0
,
{\displaystyle x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0,\,\!}
ya zi
x
2
+
b
a
x
=
−
c
a
.
{\displaystyle x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}.}
x
2
+
b
a
x
+
(
1
2
b
a
)
2
=
−
c
a
+
(
1
2
b
a
)
2
,
{\displaystyle x^{2}+{\frac {b}{a}}x+\left({\frac {1}{2}}{\frac {b}{a}}\right)^{2}=-{\frac {c}{a}}+\left({\frac {1}{2}}{\frac {b}{a}}\right)^{2},\!}
(
x
+
b
2
a
)
2
=
−
c
a
+
b
2
4
a
2
.
{\displaystyle \left(x+{\frac {b}{2a}}\right)^{2}=-{\frac {c}{a}}+{\frac {b^{2}}{4a^{2}}}.\,\!}
(
x
+
b
2
a
)
2
=
b
2
−
4
a
c
4
a
2
.
{\displaystyle \left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}.}
x
+
b
2
a
=
±
b
2
−
4
a
c
2
a
.
{\displaystyle x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}.}
x
=
−
b
2
a
±
b
2
−
4
a
c
2
a
=
−
b
±
b
2
−
4
a
c
2
a
.
{\displaystyle x=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}.}






![{\displaystyle r(\varphi )=4a{\frac {\cos(\varphi )}{\sin ^{2}(\varphi )}}\quad \ \varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e363dc1cfefcfa913c650441629796c67548e0d)










